|
第80話
不可能にまつわる話
|

「主な対象読者」
生物、宇宙、化学、物理、数学の内容を盛り込んであります。対象者は、小学生以上ですが、5章のみ高校生程度の数学の知識が必要となります。ただし、各章ともほぼ独立しておりますので、読みやすいところだけ読まれも差し支えありません。
本 文 目 次
1.子供の夢
2.いるかいないか
3.錬金術
4.永久機関
5.角の三等分
著者 坂田 明治
第80話 不可能にまつわる話
1.子供の夢
今回は不可能にまつわる話をいくつか集めてみました(不可能にまつわる話であって、必ずしも不可能の話ではありません)。2章から5章まではほぼ独立していますので、興味のある部分だけ読まれればよいかと思います。
この章では、不可能について考えていきますが、ほとんど与太話(よたばなし)です。しかし、本稿中で最も重要な部分です。前書きはこのくらいにして、本文に入りましょう。
まず、結果として不可能になったとしても、最初に可能性を信じて考えることは、必ずしも悪いことではありません。そもそも、最初から不可能であるなんて解りませんから。いろいろな人がいろいろと考え、やがてどうしてもできないところから、「不可能ではないか」と考える人が現れます。そして不可能の証明がなされるというように流れていきます。
一方で、子供は可能か不可能かなどとは考えません。その上、子供は特に鍛えた(きたえた)部分が発達するという特性を持っています(もちろんやり過ぎは害になりますが)。大人は不可能だとしてやりもしないことでも、子供にはできてしまうということが多々あります。このため、「子供は無限の可能性を持っている」といわれるのでしょうね。
大人になると知識が増えてくるため、できなさそうなものは、「こんなのできっこない」として、さっさとあきらめてしまいますね。まあこれを、可能性のないものは枝狩り(えだがり)して、無駄なことを省く(はぶく)とか、合理的に考えるとかなんとかいいます。しかし、よくよく見ると、柔軟性がなくなり、考え方の範囲が狭まって(せばまって)いるだけです。判断に要する時間を短縮するためには必要なことなのでしょうけれども。
ということで、子供の方に目を向けた方がいろいろ面白いし、参考になります。事実、昔の人は、「負うた子に教えられて浅瀬を渡る」という諺(ことわざ)を残しています。
さて、子供の頃、「将来の夢」とかなんとかを無理やり書かされた人も多いかと思います。このときに、「世界征服」とか、「人類滅亡」、「地球爆破」、「太陽の自爆」などと書くと、大体は先生に怒られます。先生も先生です。こんなこと不可能だと一瞬で解かるでしょうが。実際、こんな夢を描いても現実にやった人はいません。
それはそれとして、子供の頃、日本の裏側まで、シャベルで穴を掘ろうとした人もいるかと思います。しかし、1メートルも掘らないうちにあきらめてしまったことでしょう。これも不可能なことです。穴を掘ってみれば解かりますが、穴の側面がどんどん崩れて(くずれて)きて、掘っても掘っても深くなりません。子供には(大抵の大人も)、穴の側面を補強して、崩れなくするような土木技術を持っていません。それ以前に、側面補強なんて考えもしません。他にもいろいろと問題があって、結局、地球の裏側にまで穴を掘れません。
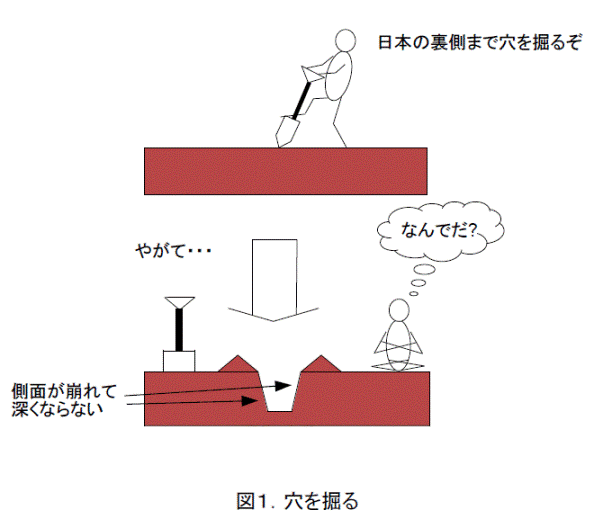
最初の「世界征服」、「人類滅亡」、「地球爆破」、「太陽の自爆」よりも、「日本の裏側までシャベルで穴を掘る」という方が、「シャベルで」という制限がついています。このことを頭の片隅(かたすみ)に入れておきましょう。
次の話は、「空を飛ぶ」という話です。ほとんどの人が、空を飛びたいと、一度は夢見たはずです。すぐに、「そんなの不可能じゃん」といわれそうですね。
しかし、必ずしも不可能ではありません。航空券買って、飛行機に乗れば飛べますよね。すると、「そんなの乗っているだけで、自分でコントロールしてないから、飛べたとはいえない」とケチがつけられます。じゃ、自分でコントロールすればいいのか。「飛行機のパイロットになれば、飛べたことになるな」との反論が出てくるでしょう。
不可能を主張する方も負けてはいませんから、「動力を使って飛ぶなんて邪道(じゃどう)だ。そんなの飛べたことにならん」と反論します。「それなら、ハングライダーなら動力を使ってないから飛べたことになるじゃないか」と更に反論するでしょう。
でも、「道具を使うこと自体が邪道だ。自分の力だけじゃないとだめだ」と続け反論します。「だったら、ジャンプすればいいんだな。これなら自力で飛んだことになるだろう」と、反論に次ぐ反論が出てきます。
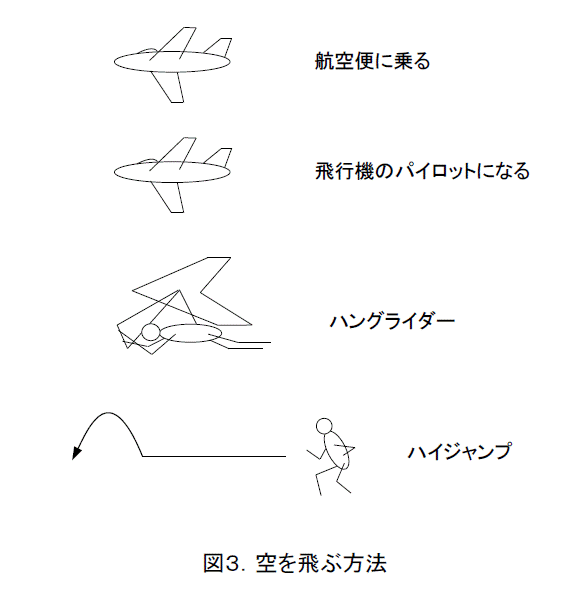
この後は、「そんなの空を飛んだことにならん」、「じゃ、空ってなんだよ。飛ぶってなんだよ」と続きます。まあ、なんとでもいえるので、この議論に果てはありません。
話がだいぶこじれてきましたね。なんでこうなったのでしょうか。よく見てみると、双方で屁理屈(へりくつ)をこねあっています。そもそも、「空を飛ぶ」ということがあまり明確になっていません。これでは、好き勝手な解釈、つまり、自分に都合のよいことばかりいえます。話がかみ合うはずもありません。
そうすると、話をかみ合わせるためには、まず、「空」ということを明確に規定しなければならないことが解ります。その上で、「飛ぶ」ために許される方法がちゃんと規定されなければなりません。これは、図3.にあるように、動力を使ってよいのか、道具を使ってよいのか、自力でないとだめなのかの規定です。
まとめると、「対象となるものは何か」がはっきりと規定されること、そして、「使える方法が何か」がはっきりと規定されることです。この2点を明確にする必要があります。
これで、不可能についてきちんと考える際は、対象となるものを明確にすることと、使える方法を明確にしなければならないことが解ります。これより、ある方法で不可能だと解っても、別の方法で可能になる場合もあります。それは後の章で出てきますのでお楽しみに。
2.いるかいないか
この章の話は生物の存在に関するものです。要するに、これこれという生物がいるかいないかという問題です。
最初に、「海坊主」がいるかいないかを考えてみましょう。
そもそも、海坊主ってなんでしょうか。なんだかよく解りませんが、とりあえず生物ということにしておきます。とはいっても、生物の定義は非常に難しく、うまく定義できるものかどうか知りません。(ここは「理科好き子供の広場」なので、一応、「妖怪」は考えないことにします)
「生物」を「生きているもの」といってみたところで、ただの言い換えにすぎません。解った気になっているだけで、実は、全然状況が変わっていません(よく、「ただのいい換え」で説明したことにする手が使われています)。これでは話が進みませんので、一般的にいわれている以下の性質を持つものを生物の定義としておきます。
(1)自己増殖能力
(2)エネルギー変換能力(物質代謝とエネルギー代謝)
(3)恒常性維持能力
「自己増殖能力」については、特に説明はいらないでしょう。勝手に、コピーを作って増えるということです。ただし、完全なコピーである必要はありません。(この原稿もバックアップと称してコピーが勝手に増殖しています)
「エネルギー変換能力」というのは、外部から物質やエネルギーを取り入れ、内部で変換し、外部に物質やエネルギーを出しているということです。だから、物質代謝とエネルギー代謝ともいえます。たとえば、光合成を考えてみると、外部から太陽光線(エネルギー)と、二酸化炭素や水などの物質を取り入れ、内部で有機物を合成し(エネルギーを使って物質の変換)、不要になったものを外部に捨てています。
「恒常性維持能力」というのは、外部の状態に関わらず、内部の状態が一定に保たれていることです。我々の体は、外が暑くても寒くても、体温を一定に保っていますよね。
話を元に戻しましょう。「海坊主」を「タコ」のことだと解釈すれば、これはいることになります。しかし、「なんだか得たいの知れないもの」と解釈すると、いるのかいないのか解らなくなります。そこで、海坊主はどんなものかを定義しなくては話しになりません。
とりあえず、なんらかの定義がされたとして、いるかいないかを考えましょう。言葉の上では、いることを示すのは簡単です。実際に見つけてくればいいのだから(本当は非常に難しい)。いないことを示すのは非常にやっかいです。見つからないということは、いないことにはならないからです。あらゆる方法で、海を隈なく(くまなく)探して、それでも見つからないということを示さねばなりません。これはほとんど不可能です。
第1に、海を隈なく探すのは無理です。海坊主が移動能力を持っているとするなら、更に難しくなります(見つかる前に逃げるから)。第2に、あらゆる方法なんてなんのことだか解りません。今知られている方法だけでなく、将来発見される方法までも(その上発見されない方法も)考えなければなりません。これは人間業(にんげんわざ)ではできません。
今度は、海から宇宙に目を向けてみましょう。宇宙に海坊主がいるかどうかどころか、今のところ宇宙に生物がいるかどうかすら解っていません。(ここで、海坊主→シーボーズ→怪獣墓場→宇宙怪獣と連想した人は、なぜ海坊主の話から始めたかが解りますよね)
一応、上のほうで書いた生物の定義を元に考えます。まず、宇宙生物なんて誰も見たことはないので、どんなものか解りません。とりあえず、生息できそうなところを考えてみましょう。宇宙空間にふわふわ漂って(ただよって)いるとは考えにくいでしょう。真空に近い状態なので、必要な物質を手に入れにくいからです(物質代謝がしにくい)。そうすると、天体の方にいる可能性の方が高いと考えられます。それでは太陽はどうでしょうか。あまりにも環境が苛酷(かこく)なので、いる可能性は低いと考えられます(恒常性の維持が難しい)。そうなってくると、惑星か、衛星の方がいる可能性は高くなります。現在、太陽系内の天体はいろいろと調べられ、その目的の一つに、生物の痕跡(こんせき)の調査があります。見つかると面白いのですが。
太陽系内の惑星や衛星は、探査機を飛ばして調べるなど、いろいろな手があります。ただし、いまだに見つかってはいません。地球には生物がいるのだから、地球に近い環境の方が生物のいる可能性は高いと考えられます。そうすると、太陽系内を探すよりも、他の太陽系を探した方がいいかも知れません。そういう意味もあって、系外惑星(他の太陽系にある惑星のこと)の調査が行われています。
まずは、系外惑星の発見です。実際に、系外惑星はかなりの数が発見されています。今後も発見は続くでしょう。そして、地球に似た環境の惑星が見つかれば、生物のいる可能性もでてきます。では、どうやって系外惑星を発見するのでしょうか。常識的に考えると不可能と思えるでしょう。この太陽系でも昼間は惑星が見えませんからね。大体、惑星なんて暗くて小さいし、主星(太陽のこと)の光に邪魔されて見えそうな気がしません。
しかし、直接観測できなくても、間接的な観測はできます。よく知られている系外惑星の見つけ方は二つあります。
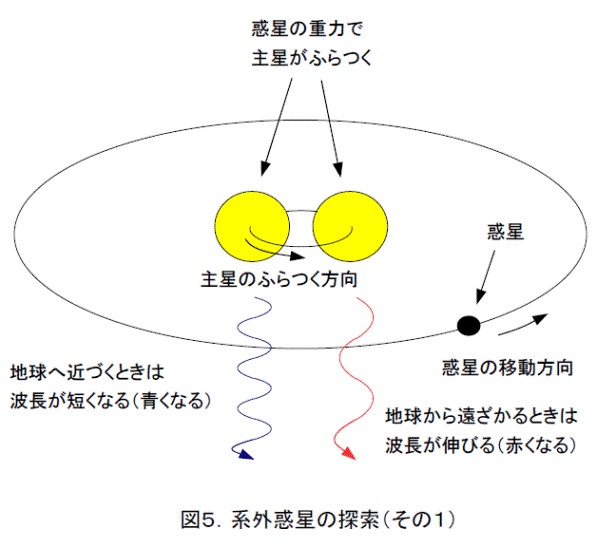
系外惑星の発見方法の一つめは(図5)、惑星の重力によって主星が引っ張られて、ふらつくことを利用した観測方法です。主星が円軌道上を運動していると考えてください。そうすると、地球に近づくときは、光が青い方へずれ、地球から遠ざかるときは、光が赤い方へずれます(この現象は、第38話 「光や音の話」に説明があります)。これから、周期的に光の波長が変化すれば、惑星があると考えられます。
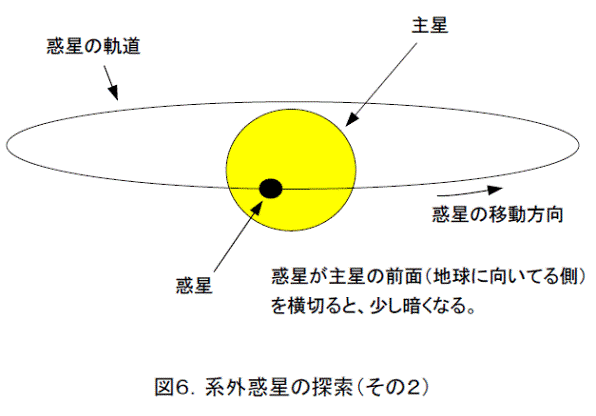
系外惑星の発見方法の二つめは(図6)、惑星が主星の前面(地球に向いてる側)を横切っている場合の観測方法です。惑星が主星の前面を横切ると、主星が少し暗くなります。これから、主星が周期的に暗くなるようであれば、惑星があると考えられます。
以上のようにして系外惑星を探索していますが、いずれも変化は極わずかですので、超高感度の観測機器が必要です。地球型惑星はたくさんありそうですから、やがて生物のいそうな系外惑星が発見されかも知れません。楽しみですね。
3.錬金術
まず、金属精錬技術は非常に歴史が古いということを頭に入れておきましょう。でないと、大昔から錬金術があったということに納得がいかないでしょう。
最初は、自然界に金属状態で産出している金、銀、銅などを拾って使っていたようです。現生人類は誕生した頃から、珍しい石として拾ってきた可能性がありますね。銅を溶かす技術は、紀元前3000年頃に開発されたようです。同じく、鉄の利用も、紀元前3000年頃のようです。
さて、今も昔も、人間の本質なんて変わっていませんから、当然欲の皮が突っ張ってました。また、大昔から金の価値は高いので、当然のように、安い金属から金を作れば大もうけができると考えられていました。要するに、錬金術でぼろもうけしようということです。
しかし、錬金術によってもたらされたものは、暗黒時代でした。化学の発達が阻害(そがい)されていたのです。諸悪(しょあく)の権化(ごんげ)は、「秘密主義」にありました。自分だけぼろもうけしたいがため、錬金術の技法はすべて秘密でした。これは自然科学の思想とは相反するものです。
情報公開されていないということで、誰がやっても同じ失敗を、それを何千年もの長期間に渡って繰り返していました。知識の蓄積もなにもあったものではありません。これを暗黒時代といわずして、なにを暗黒時代と呼ぶのでしょうか。(錬金術をかかげた詐欺師もかなりはびこっていました。オレオレ詐欺にしろ、何とか詐欺にしろ、いつの時代、どんな世界でも詐欺師ははびこっているなぁ)
まあ、錬金術師の中には、「不可能」であることを悟り、蓄積した技術で薬品の製造を始めた人たちもいたようですが。そういえば、「万有引力の法則」や「運動の法則」などで、自然科学に多大な貢献をしたアイザック・ニュートンも錬金術にはまっていました。偉人といえども過ち(あやまち)をおかすということでしょうか。
話は変わって、紀元前5世紀頃、レウキッポスとその門人デモクリトスによって原子論が展開されていきました。これを簡単に書くと、これ以上分解できない「アトモス」というものがあって、それが空間中を運動している。そして、すべてのものは、アトモスの離合集散(りごうしゅうさん)だというのです。そして、このアトモスが現在の原子(atom)につながりますが、この後しばらく発展したものの、アリストテレスの四元素説と、キリスト教の勢力拡大によって、暗黒時代に落ちていきます。
四元素説というのは、「万物は土、水、風、火からできている」というものです。錬金術師にとっては、まことに都合のよい説ですね。だって、土、水、風、火をうまく組み合わせれば、金を作り出せるじゃん。
何千年もの間続いた暗黒時代に、光をもたらす上で、決定的な役割を果たした人物がロバート・ボイルです。ボイルは、「誰がやっても常に同じ結果を、誰がやっても常に確かめられる実験的事実に基づいて実証する必要がある」と考えていました。
ボイルは、「ボイルの法則」の発見者として有名です。これ、気体は温度が一定のとき、
(気体の圧力)×(気体の体積) = 一定
という法則です。たとえば、体積を半分すると圧力が2倍になります。
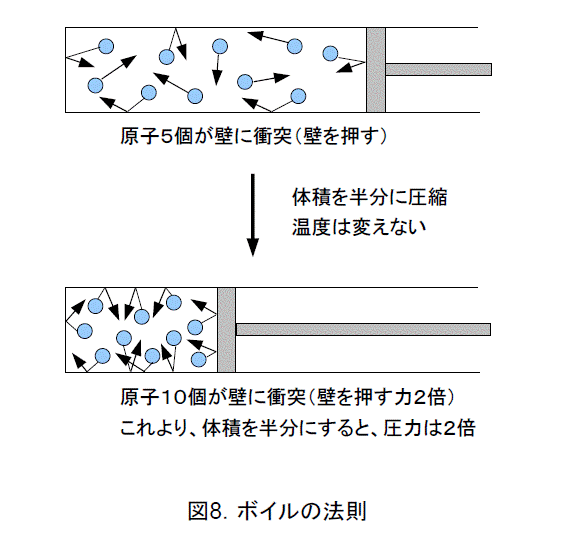
原子論の立場から、この法則はうまく説明できます。
そして、気体は液体や固体に変化しますので、気体が原子でできているとすると、液体や固体も原子でできていると考えられる。こうして、すぐれた考察を通して、原子論が復活していきました。
追試可能な実験によって実証された事実のみを尊重するということから、化学の方法論が確立されたため、後に多くの化学者によって多大な発見がもたらされました。それゆえ、ボイルは「近代科学の父」と呼ばれています。
この後、紆余曲折(うよきょくせつ)を経て、「現代科学の父」であるアントワーヌ・ラボアジェの登場となります。この頃になると、いろいろな化学者の働きによって、「水素」や「酸素」が発見され、水素を燃焼させると「水」ができることが発見されました。
2H2 + O2 → 2H2O
また、赤熱した鉄に水蒸気(とにかく水です)を通すと、水素ができることから、水が元素ではないことが証明されました(分解できるから)。
Fe + H2O → FeO + H2
ここにアリストテレスの四元素説はとどめを刺されましたね(水が元素じゃないから)。
ラボアジェは天秤(てんびん)を用いた正確な測定の重要性を認識していました。さまざまな実験を繰り返していくうちに、化学反応によって物質の総量は変化しないことを実証しました。そして得た結論は、「質量は発生したり消えたりするものではなく、ある物質から別の物質へ移動するだけ」です。これが、「質量保存の法則」と「物質保存の法則」です。
要するに、「鉄」は「鉄」であり(元素)、「金」は「金」であり(元素)、「鉄」から「金」をつくることなんてできない(金は化合物ではない)ということです。
ここまでの説明で、途中をかなりはしょっています。簡単に調べられますので、化学史を調べてみると楽しいですよ。
ここまでで「化学反応」では、「錬金術」が不可能であると解りました(解るほどちゃんとは書いてませんが)。「化学反応」でだめなら、別の方法ですよね(「質量保存の法則」と「物質保存の法則」から解き放たれる必要があるということ)。というわけで、核反応を利用する方法が考えられます。
(1)核分裂
(2)核融合
核分裂を利用するなら、金より原子番号の大きい元素を核崩壊させればよいことになります。水銀にγ線(ガンマせん)を当てれば金ができるという話をどっかで聞いたことがあります。早速、周期律表を見てみましょう。金は79Au、水銀は80Hgと書かれていました。ということはβ+崩壊(ベータプラスほうかい)ですね。
80Hg + γ → 79Au + e+ + ν
γ:γ線、 e+:陽電子、ν:ニュートリノ
これは陽子が中性子に変わっているので、その部分だけ書くと、
p + γ → n + e+ + ν
p:陽子、 n:中性子
となります。
しかし、この方法は実用的ではありません。水銀から金はできるものの、莫大な費用がかかってしまいます。つまり、ぼろもうけするどころか、大損してしまいます。
核融合を利用して金を作る方法は今のいまのところ無理です。鉄26Feまでは、核融合によってエネルギーを発生しますが、それ以上はエネルギーを投入しないと核融合が起こりません。ただでさえ核融合は難しく、投入したエネルギー以上のエネルギーが得られなくて四苦八苦しているのですから。
それでは、どのような状況で、核融合によって金が作り出されるかというと、「太陽の自爆」です。人間業でできるようなものではありません。
4.永久機関
永久機関は、なんとなくできそうな気がしたためか、錬金術よりよほど人気があったようです。全財産をつぎ込んで製作しようとして失敗し、貧困に陥った(おちいった)人もかなりいたと聞きます。しかも、いまだに永久機関ができると信じている人もいるようです。
まず、我々は物理法則に従っているということを頭に入れておきましょう。これははっきりした規定になっています。空想など、物理法則による規定がない世界では、変身して巨大化するなど、なんでもありです。
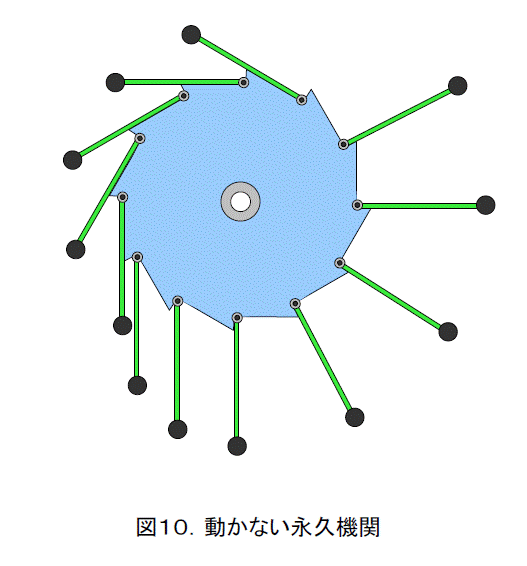
図10は動かない永久機関の例です。いろいろなところで出てくるので、見たことのある人も多いかと思います。この構造は、歯車みたいな車輪のふちに、おもりを付けた自由に動く棒をとりつけたものです。そして、右側のおもりは、左側のおもりよりも中心から遠いので、常に右半分は、左半分を引っ張って動くというものです。
しかし、図10をよく見ると、右側のおもりは4個で、左側のおもりは7個(1個は左右の中心線上)です。右側のおもりの数は、必ず左側のおもりの数より少なくなります。そして、どこかの位置で右半分と左半分は釣り合ってしまいます。要するに、たとえ動かしても、やがて釣り合いの位置で止まるということです。これは天秤の釣り合いと同じ原理です。詳しく知りたい人は、力のモーメントの勉強をしましょう。モデルをきちんと決めれば、釣り合いの位置も計算できますよ。
永久機関の例は、何万あるのか解らないぐらいたくさんあります。しかも、結構美しいものもあり、人寄せのためにショーウィンドーに飾られて動いていたりします。もちろん、解らないように後ろにモーターなどがついていて、それで動かしています。
さて、永久機関というものは、他からエネルギーを受けることなしに動き続け、しかも外部に対してなにらかの仕事をするというものです(これを第一種永久機関といいます)。これを作り上げようとするあらゆる試みはすべて失敗に終わりました。やがて エネルギーは、発生したり消えたりするものではなく、総量は変化しないこと、つまり「エネルギー保存の法則」が確立されました。なんか、錬金術師のところで出てきた、「質量保存の法則」と「物質保存の法則」と似てますね(もっもと、エネルギー保存の法則の方が強力で、核反応によっても破られません)。
似ているといえば、ここでも、錬金術師のときと同様に詐欺師がはびこっています。「あと少しで永久機関が完成するから出資してくれ。完成の暁(あかつき)にはエネルギー問題は解決するから」とか、「全世界のエネルギーを支配できる」とかなんとか。まっ、いろいろな手口があるようですが。
エネルギー保存の法則が確立されたからといって、永久機関推進者はあきらめませんでした。もちろん、エネルギー保存の法則を理解してない人は論外です。今度は、エネルギー保存の法則を破らないような永久機関を考えようとしました。エネルギーの総量が変わらなければいいんだから、熱エネルギーを取り出して仕事をし、仕事で発生した熱を返してやればよいという発想です。熱のリサイクルですね。
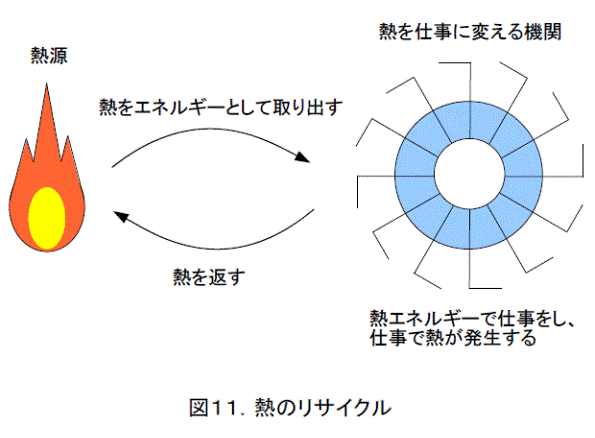
図11をよく見てみましょう。もし、永久機関ができたとすると、熱を完全に仕事に変換しなくてはなりません。そうでなければ、熱がどこかへ逃げてしまいます。すると仕事を熱に変換して熱源に戻しても、熱の量が減ってしまいます。これでは、やがて熱がなくなって機関は動かなくなってしまいます。ということは、永久機関は、熱エネルギーを100%仕事に変えて、またこの仕事を熱に変換し、熱をリサイクルするものだということになります。なお、仕事を熱に変換するのは簡単です。摩擦(まさつ)が働くようにすればいいからです。
上に書いたように、エネルギー保存の法則に反しない永久機関を「第二種永久機関」といいます。
しかしながら、結局のところ、第二種永久機関は作れませんでした。こうして、第二種永久機関の実現が否定されて、「熱力学第二法則」が確立しました。
この法則はいくつかの表現がありますが、内容は等価です。すなわち、どれか一つを仮定すれば、他が導き出せるということです。
熱力学第二法則:
(1) 永久機関(第二種永久機関)は実現不可能
(2) 熱を完全に仕事に変えるサイクルは存在しない
(3) 仕事を加えずに、熱を低温から高温に流すことはできない
(4) エントロピー増大の法則
今までのことから、(1)と(2)はいいでしょう。(3)は冷蔵庫やクーラーみたいに、外部から仕事を加えないと、低温から高温に熱を捨てて(流して)冷やせないということです。(4)は少し解りにくいかも知れません。まず、乱雑さの程度を表している指標がエントロピーというものです。そして、エントロピー増大の法則を噛み砕いて書くと、自然界の系は、乱雑さが増大する方向に進む傾向があるということです。いい加減なたとえで説明すると、ほっておくと自分の部屋が散らかって乱雑になるということです(掃除や整理をしないでほっておいて、「エントロピー増大の法則の実験中」というと怒られますよ)。まあ、この辺は自分で勉強して、ちゃんと理解しましょう。
いきなり熱力学第二法則が出てきましたが、実は、すでに「熱力学第一法則」は出ています。熱力学第一法則は「エネルギー保存の法則」です。ついでに、「熱力学第三法則」というのもあります。これは「絶対零度には到達できない」という法則です。
熱力学第一法則と熱力学第二法則を見比べてみましょうね。ここまでの話をよく見ると、熱力学第一法則(エネルギー保存の法則)は、可能な現象がなんであるかを示す法則です。たとえば、第二種永久機関を否定しません。それに対して、熱力学第二法則は、実際に起きる現象を示しています。熱力学第二法則の表現のところを見れば解ると思いますが、可能である現象のうち、実際に起こるものは限られているということです。
まあしかし、自然現象を理解するには、これだけでは足りません。もっといろいろな知識が必要です。ここから先は自分で勉強しましょう。
ところで、永久機関ができると信じている人たちは、いろいろと屁理屈を付けて、なんとかしてできるように見せようとしているようです。慣性の法則(物体は、外力が働かない限り、等速直線運動を続ける)とか、角運動量保存の法則(たとえば、地球が地軸を中心に自転を続けること。フィギュアスケートで、回転しているときに、手を縮めると回転が速くなるのもこの法則)とかなんとか、永久機関に変な結び付けをしていたりします。
更に、エントロピー増大の法則に引っ掛けて、「乱雑さが増大するなら、生物みたいな複雑なものができるはずがない」とか、「もっと簡単に、乱雑さが増大するなら、分子が揃って(そろって)結晶(秩序だっている)ができるはずがない」と屁理屈を付けたりもします。
少し前に書いたように、自然現象は熱力学の法則だけでは足りません。たとえば、結晶は、力学的エネルギーを最小化するようにできます。一般的に、力学的エネルギーの最小化と、エントロピーの最大化のバランスが取れた状態になります。先に書いたように、いろいろ勉強して自分で考えましょう。
どうでもいいといえばどうでもいいのですが、「永久機関ができた」などといって持ってこられると、いちいちその間違いを見つけて指摘しなくてはならず、これは精神衛生上よくありません。それでなのかどうかは解りませんが、永久機関は特許になりません。特許庁のページ(下記URL)に、発明に該当しないと書いてあります。多分、いちいちそんな間違いを指摘するよりも、さっさと切り捨てた方が面倒がなくていいからだろうと思います。
5.角の三等分
この章は、実際に身をもって不可能を示す苦労を楽しむ(苦しむ)ためのものです。
取り扱うのは角の三等分問題です。これは、定規とコンパスだけで角を三等分できるかという問題です。こういう問題では、ある特定の角を三等分するのではなく、一般の角を三等分することを考えます。
まあ、有名な問題なので、定規とコンパスだけで角を三等分できるかと聞くと、大概の人は「不可能」と答えるでしょう。この回答は正しくありません。定規とコンパスだけで角を三等分する方法はあります。アルキメデスの角の三等分法というものがあるからです。
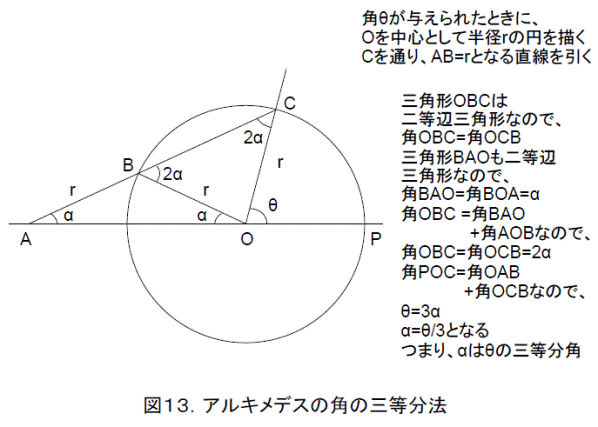
図13を見れば、三等分角ができています。これを作図に利用したものが図14です。
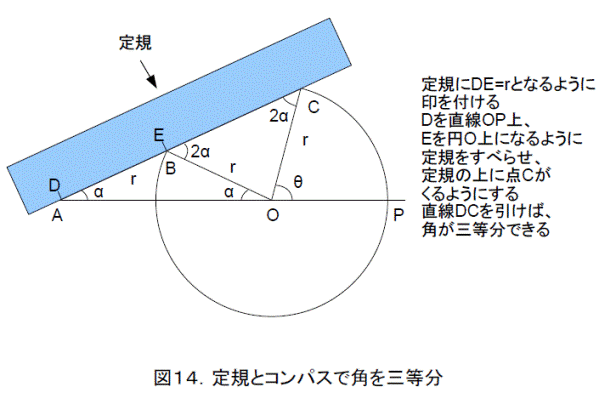
これでは、「定規とコンパスだけで角の三等分は不可能」といってることと合いませんね。なぜこんなことになったのでしょうか。
我々は、「定規とコンパスだけで」というと、それだけで、定規とコンパスだけでできることが規定されていると錯覚してしまいます。定規とコンパスなんて、それこそ無限の用途があります。たとえば、子供の頃、コンパスの足を広げ、手裏剣として投げていたし、定規でチャンバラをやっていたりしました。
そこで、何度も書いていますが、定規とコンパスでできる作図を規定しなくては不可能の話ができません。特にこの場合は、3章や4章のように自然界の法則によって自然に制約がかかるわけではありませんから。
では、定規とコンパスだけで作図するというのは、どういことであるか、明確に規定しましょう。(以下、複雑になることを避けるため、細かい条件や場合分けは書きません。自分で補いましょう)
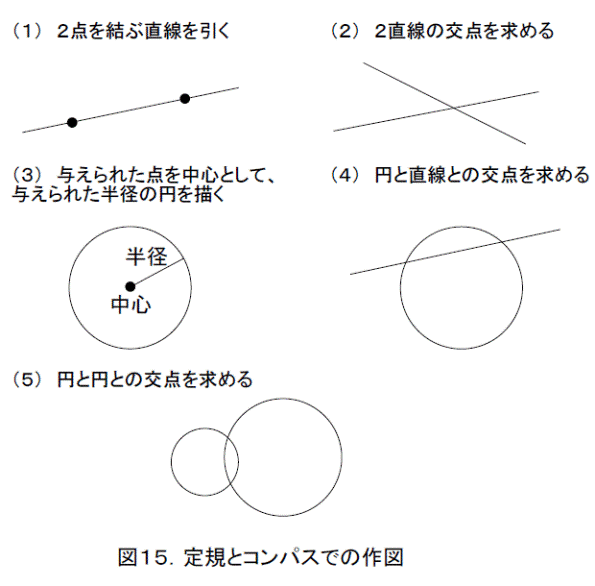
図15にある一連の手順を有限回組み合わせることが、定規とコンパスで作図するということです。
あとで使いますので、垂線と垂線の足、平行線の作図法を図16、図17に書いておきます。これらが、それぞれ垂線や平行線になっている理由は自分で考えましょう。
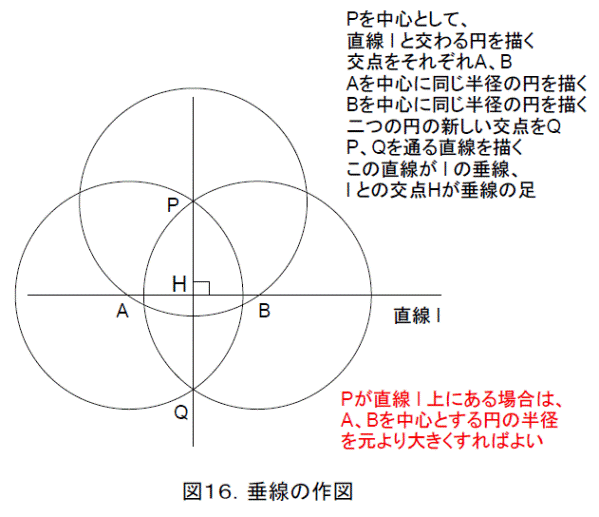
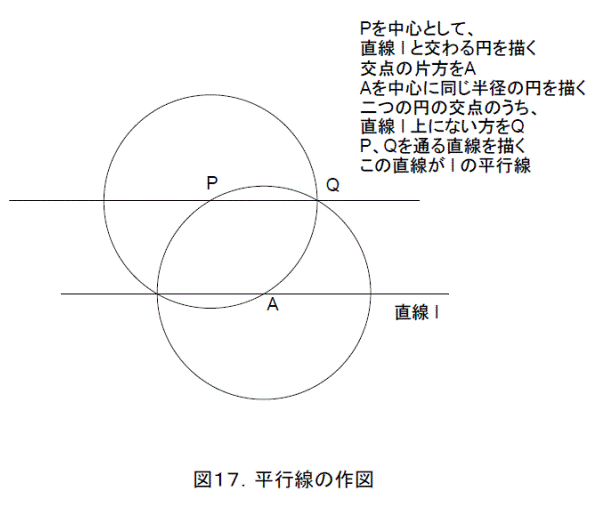
垂線と平行線が作図できれば、四則演算と平方根が作図できます。
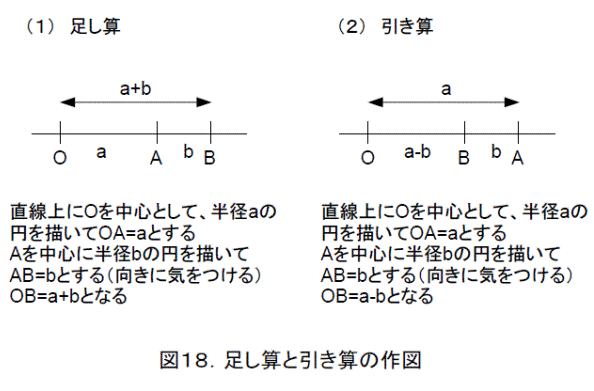
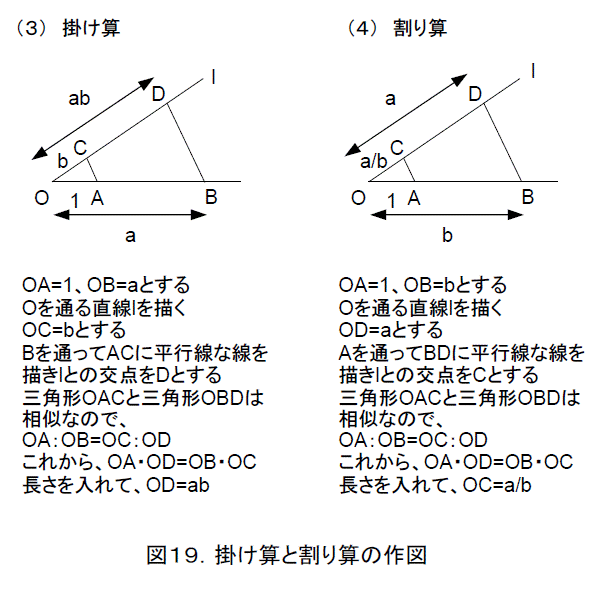
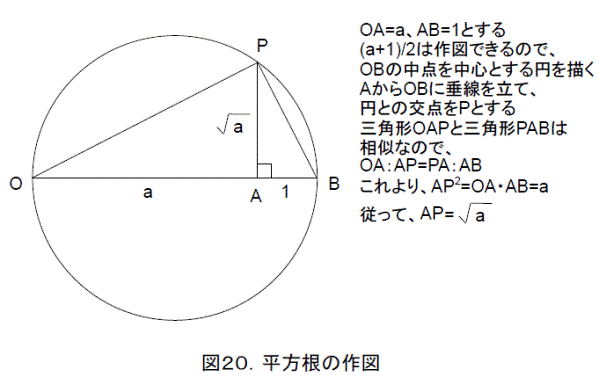
すると、有理数は1から始めて、四則演算で作れるので、有理数はすべて作図できることになります。さらに、平方根が作図できるので、有理数に四則演算と平方根を何回か組み合わせて作った数もすべて作図できることになります。たとえば
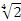 は2の平方根のそのまた平方根をとったものだから作図できます。また、 は2の平方根のそのまた平方根をとったものだから作図できます。また、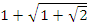 なども作図できます。 なども作図できます。
今度は代数的な側面から見ていきます。
出発点は有理数です。有理数は、四則演算が自由にできます。このように四則演算が自由にできる体系を「体(たい)」といいます。体については、そこいら中に解説が転がっていますので、自分で勉強してみてください。
既に見たように、有理数はすべて作図できます。ここでは、図15を見直しながら話を進めていきます。
図15の(1)は、平面座標で、点(a,b)、(c,d)が与えられたときに、その2点を通る直線が描ける(作図できる)ということです。直線の方程式は簡単に求まります。
実際に求めると、(b-d)x+(c-a)y+(ad-bc) = 0となります(自分で計算して求めましょう)。この式から、a、b、c、dが有理数のとき、直線の方程式の係数は有理数となります。
図15の(2)は2本の直線の交点は求まるということです。求まるということは作図できるという意味です。求めた点から、それぞれ、y軸、x軸に垂線を下ろすとx、y座標となりますので、x、y座標は作図できる数ということになります。係数が有理数である2本の直線px+qy+r = 0、sx+ty+u = 0の交点は、p、q、r、s、t、uから四則演算によって作られたものになります(自分で解いて確かめてください)。つまり有理数です。ということは、2直線の交点の座標は有理数であって、新しい数にはなりません。
図15の(3)は、点(a,b)と半径rが与えられたときに、円が描ける(作図できる)ということです。円の方程式は、
(x-a)2+(y-b)2 = r2
ですから、
x2+y2-2ax-2by+(a1+b2-r2) = 0
となります。これから、円の方程式の係数も有理数です。
図15の(4)は、直線と円の交点が求まるということです。直線の方程式ax+by+c = 0、円の方程式x2+y2+px+qy+r = 0(a、b、c、p、q、rは有理数)の交点は連立方程式を解けば求まります(自分で計算して求めましょう)。
解いてみれば解りますが、x = d+e
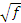 、y = g+h 、y = g+h 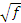 (d、e、f、g、hは有理数)という形になります。 (d、e、f、g、hは有理数)という形になります。
ここで、u+v
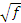 、s+t 、s+t 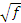 (u、v、s、tは有理数)という形の数を考えてみましょう。これらは四則演算について閉じています。 (u、v、s、tは有理数)という形の数を考えてみましょう。これらは四則演算について閉じています。
(u+v
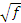 )+(s+t )+(s+t 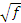 ) = (u+s)+(v+t) ) = (u+s)+(v+t) 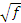
(u+v
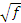 )-(s+t )-(s+t 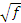 ) = (u-s)+(v-t) ) = (u-s)+(v-t) 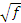
(u+v
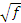 )(s+t )(s+t 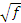 ) = (us+vtf)+(ut+sv) ) = (us+vtf)+(ut+sv) 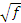
(u+v
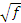 )/(s+t )/(s+t 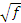 ) = (us-vtf)/(s2-t2f)+(sv-tu)/(s2-t2f) ) = (us-vtf)/(s2-t2f)+(sv-tu)/(s2-t2f) 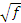
つまり、四則演算の結果はすべてm+n
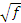 (m、nは有理数)という形になります。ということで、m+n (m、nは有理数)という形になります。ということで、m+n 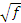 (m、nは有理数)という形の数全体は体になります。もちろん、この形の数は作図可能です。 (m、nは有理数)という形の数全体は体になります。もちろん、この形の数は作図可能です。
また、
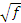 が有理数にならないとき(たとえば が有理数にならないとき(たとえば 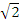 )、m+n )、m+n 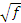 の形の数よりなる体Fは、有理数を含みます(n = 0ときが有理数となるから)。このような場合、Fを有理数体の拡大体、有理数体をFの部分体といいます。以下、含む方の体を拡大体、含まれる方の体を部分体と呼びます。 の形の数よりなる体Fは、有理数を含みます(n = 0ときが有理数となるから)。このような場合、Fを有理数体の拡大体、有理数体をFの部分体といいます。以下、含む方の体を拡大体、含まれる方の体を部分体と呼びます。
図15の(5)は、円と円の交点が求まるということですが、これは(4)に吸収されてしまいます。円の方程式x2+y2+ax+by+c = 0、x2+y2+px+qy+r = 0(a、b、c、p、q、rはすべて有理数)を考えて、最初の式から後の式を引くと、(a-p)x+(b-q)y+(c-r) = 0となります。これは直線ですので、結局は、円と直線の交点を考えていることと同じになります。
今までの考察を一般化してみましょう。まず、有理数体をF0とします。もちろんF0の要素は作図可能です。Fkが作図可能な数よりなる体のとき、Fkの要素wで
 がFkに含まれないときに、u+v がFkに含まれないときに、u+v  (u、vはFkの要素)という形の数全体からなる体をFk+1とします。いままでやってきたことから、Fk+1の要素は作図可能で、Fkの拡大体になっています。 (u、vはFkの要素)という形の数全体からなる体をFk+1とします。いままでやってきたことから、Fk+1の要素は作図可能で、Fkの拡大体になっています。
ここまでくると、作図可能な数かどうかを判定する方法ができます。定規とコンパスで作図できるというのは、図15にある操作を有限回行ってできることですから、
数xが作図可能であることは、
F0、F1、・・・、Fk
Fkはxを要素として含む
という拡大体の有限列が存在することとなります。
さて、これだけのことが解ったのだから、少し応用してみましょう。
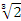 が作図不可能であることを確かめてみます。これ、立方体の体積を2倍にするような辺は、定規とコンパスで作図不可能であるという問題です。 が作図不可能であることを確かめてみます。これ、立方体の体積を2倍にするような辺は、定規とコンパスで作図不可能であるという問題です。 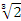 は方程式、 は方程式、
x3-2 = 0
の解となります。
ここで、
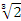 が作図可能であるとすると、 が作図可能であるとすると、
F0、F1、・・・、Fk (
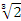 は Fk に含まれる) は Fk に含まれる)
となる拡大体の有限列が存在します。
まず、
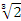 は無理数ですから、F0、には含まれません( は無理数ですから、F0、には含まれません( 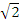 が無理数であることと同じように示せますので、自分でやってください)。これを念頭におきましょう。 が無理数であることと同じように示せますので、自分でやってください)。これを念頭におきましょう。
上の方程式の解x(
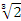 のこと)が初めてFkでできたとします。つまり、Fk-1までには含まれず、Fkに含まれるということです。 のこと)が初めてFkでできたとします。つまり、Fk-1までには含まれず、Fkに含まれるということです。
そうすると、
x = u+v
 (u、v、wはFk-1に含まれ、 (u、v、wはFk-1に含まれ、  はFk-1に含まれずFkに含まれる) はFk-1に含まれずFkに含まれる)
と書けます。
このとき、
y = u-v

も、x3-2 = 0の解になります。
x3-2を計算すると(自分で計算してください)、
x3-2 = s+t
 (s、tはu、v、wの多項式) (s、tはu、v、wの多項式)
となり、
y3-2 = s-t

となります。
x3-2 = 0だから、s+t
 = 0です。 = 0です。
tが0でないとすると、
 = -s/tとなってしまうので、 = -s/tとなってしまうので、
 はFk-1に含まれます(Fk-1は体だから)。 はFk-1に含まれます(Fk-1は体だから)。
 のとり方に反するのでt = 0。これからs = 0。 のとり方に反するのでt = 0。これからs = 0。
従って、y3-2 = 0となって、yもx3-2 = 0の解です。
xとyは異なるので、x3-2 = 0の実数解が2個あることになります。
しかし、x3-2 = 0の解は、実数解1個と虚数解2個なので矛盾します(自分でx3-2 = 0を解いて、解をよく見てみましょう)。
ということで、xすなわち、
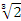 を含むようなFkは存在しません。つまり、 を含むようなFkは存在しません。つまり、 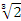 は作図不可能です。 は作図不可能です。
いよいよ、定規とコンパスで、角の三等分が作図不可能であることを示す段階にきました。
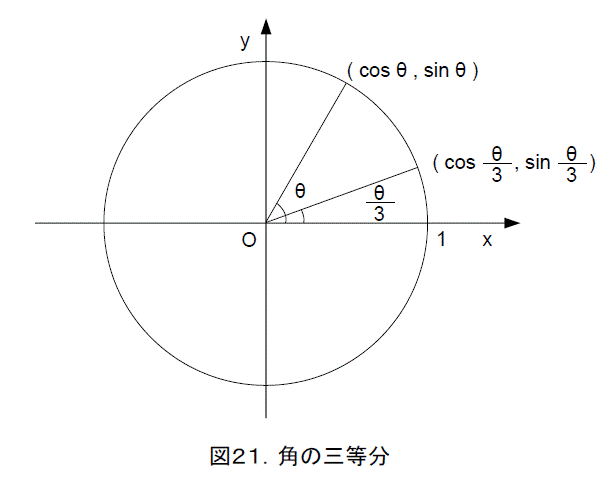
図21から、角の三等分問題は、(cosθ,sinθ)から(cos(θ/3),sin(θ/3))を求めることです。三倍角の公式(高校の数学の教科書に書いてあります)から、
cosθ = 4cos3(θ/3)-3cos(θ/3)
となります。
x = cos(θ/3)とおくと、
4x3-3x-cosθ = 0
という3次方程式ができます。
この3次方程式の解に作図できないものがあればいいので、計算を簡単にするためにθ = 60度とします。すると、cosθ = 1/2なので、
8x3-6x-1 = 0
となります。
あとは、この3次方程式の解が作図できないことを示せばいいわけです。やり方は
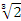 が作図できないことを示すやり方とまったく同じです。 が作図できないことを示すやり方とまったく同じです。
まず、有理数の解を持たないことを示します。
仮に有理数の解を持ったとして、x = p/q(p,qは互いに素な整数で、q>0)とおきます。
すると、
8p3-6pq2-q3 = 0
これより、
q3 = 8p3-6pq2
だから、qは偶数となります。
q = 2mとおくと、
8m3 = 8p3-24pm2
これより、
p3 = m3+3pm2
mを偶数とすると、右辺は偶数なのでpは偶数となります。
これはp,qは互いに素としていることに反します。
mを奇数とすると、pが偶数のときは、左辺が偶数で右辺が奇数となり矛盾しますし(それ以前に、p,qは互いに素に反している)、pが奇数のときは、左辺が奇数で右辺が偶数となり、いずれにしても矛盾します。
以上から、8x3-6x-1 = 0は有理数の解を持ちません。
次に、8x3-6x-1 = 0が作図可能な解を持ったとします。有理数でないことは解っていますので、
F0、F1、・・・、Fk
となる拡大体の有限列が存在します。
ここで、kは8x3-6x-1 = 0の解が入る最小の整数とします。
前と同じように、
x = u+v
 (u、v、wはFk-1に含まれ、 (u、v、wはFk-1に含まれ、  はFk-1に含まれずFkに含まれる) はFk-1に含まれずFkに含まれる)
と書けます。
代入して、
8x3-6x-1
= 8(u+v
 )3-6(u+v )3-6(u+v  )-1 )-1
= (8u3+24uv2w-6u-1)+(24u2v+v3w-6v)

前と同じように、y = u-v
 とおくと、 とおくと、
8y3-6y-1
= (8u3+24uv2w-6u-1)-(24u2v+v3w-6v)

となります。
8x3-6x-1 = 0だから、(8u3+24uv2w-6u-1)+(24u2v+v3w-6v)
 = 0です。 = 0です。
24u2v+v3w-6vが0でないとすると、
 = -(8u3+24uv2w-6u-1)/(24u2v+v3w-6v) = -(8u3+24uv2w-6u-1)/(24u2v+v3w-6v)
となってしまうので、
 はFk-1に含まれます(Fk-1は体だから)。 はFk-1に含まれます(Fk-1は体だから)。
 のとり方に反するので24u2v+v3w-6v = 0。これから8u3+24uv2w-6u-1 = 0。 のとり方に反するので24u2v+v3w-6v = 0。これから8u3+24uv2w-6u-1 = 0。
従って、8y3-6y-1 = 0となって、yも8x3-6x-1 = 0の解です。
ここで、3次方程式の解と係数の関係を使います。一般的に、
ax3+bx2+cx+d = a(x-α)(x-β)(x-γ)
のとき、
α+β+γ = -b/a
となります(展開して両辺を比較すれば解ります)。
8x3-6x-1 = 0に戻って、x、y、αを解とすると、
x+y+α = 3/4
ですので、
2u+α = 3/4
これから、
α = 3/4-2u
Fk-1は体ですので、α(= 3/4-2u)を含みます。
ということは、8x3-6x-1 = 0の解がFk-1に含まれることになります。
これは、Fkのとり方、すなわち、kは8x3-6x-1 = 0の解が入る最小の整数としたことに反します。
以上から、8x3-6x-1 = 0は作図可能な解を持ちません。つまり、定規とコンパスで角の三等分は不可能ということになります。
いやはや、不可能であることを示すのは大変でしたね。本稿の最初の方に書いたように、最初から不可能であることなんて解りません。いろいろ考えて、どうしてもできないと思い始めてからも、更に、いろいろな概念が整備されて、その上で確立するものです。これが、最初の方に書かれている、「結果として不可能になったとしても、最初に可能性を信じて考えることは、必ずしも悪いことではない」という理由です。
大人になって、できなさそうなものを、「こんなのできっこない」とすぐにあきらめてしまうのはどうでしょうか。それでいい場合もありますが、やはり納得がいくまで考えるべきではないでしょうか。本文を読まれた方は、どう感じられたでしょうか。
完
平成22年12月17日
著作者 坂田 明治(あきはる)
|