|
第123話
フィボナッチ数列の続き
|

「主な目的」
今回は、かねてより考えていた失敗体験の実施を試みています。さんざん考えて努力したのに、結果がうまく行かなかったということへの挑戦です。コスパやタイパは度外視しており、失敗から、何かを学べなければ何も残りません。
本 文 目 次
1.どうでもいい話
2.一般項
4.項と項番の関係
著者 坂田 明治
第123話 フィボナッチ数列の続き
1.どうでもいい話
暑かったのと、環境破壊が進んでいるからなのか、鳥も虫も少なくなってきた。今年は、セミも減っているらしく、鳴き声もあまりの聞こえなかった。いつもならいるはずの所にドブガモはいなかった。何が起こっているのだろうか。
まあ、ともかく、庭を見てみると、こんな奴らがいた。

写真1はネペンテスの一種に、カマキリがとまっている。夏の間も、食虫植物のところに色々なやつがいた。ツボのところに蜘蛛の巣張ってるやつもいたが、写真を撮ってなかった。
他にも、アマガエルのやつが、サラセニアのツボを住処にしていた。

こいつ、飽きてくると、その隣のツボに引っ越しやがった。

アゲハのやつも、よく庭にきていた。こいつら、仲間同士で相当仲が悪いらしく、年がら年中喧嘩していた。写真4のアゲハは、色々あったらしく、羽根がぼろぼろになっている。しかし、これはまだましな方で、もっとぼろぼろなのもいたが、写真に撮れなかった。

ギンヤンマも来たが、こいつ、自分の身体と同じ色のバラにとまっている。

少し涼しくなってからは、ドブガモが見られるようになった。

写真6はコロッとして、えらく可愛いドブガモだ。ドブガモのオスメスを見分ける方法は知らないけど、仮にこいつがメスとして、人間に当てはめると、可愛い女の子には、ろくでもない兄ちゃんが付いているもんで、やっぱり写真7のような奴が付いていた。

アヒルや犬などの動物を飼ったことがあればわかるが、人間が見ても可愛いメスがオスにモテる(オスが寄ってくる)。なんか、そういう感覚は同じなのかも知れないなー。
それはともかく、写真7を見ればわかるが、この二羽は顔が違っている。これも、アヒルを複数羽まとめて飼ったことがあれば知っているだろうが、顔も性格もみんな異なっている。むしろ、人間の方が。。。
2.一般項
元々、フィボナッチ数列については、第122話で終わりにする筈でした。 しかし、大人の事情で続きを作らねばならなくなりました。特に、一般項を求めたくなかったのだけど。そもそも、一般項を出してしまうと面白味がなくなるのだが。
とにかく、フィボナッチ数列の一般項を求めることにします。第122話の続きなので、第122話を読まれていることを前提とし、そこで使っていた記号や文字を使います。なお、ここでの一般項の求め方は第115話を読んでいると簡単です。
まず、フィボナッチ数列は式(1)のように書けます。
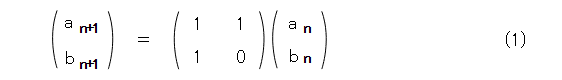
そこで、式(2)のようにおきます。
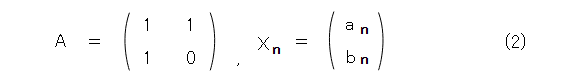
すると式(3)のようになります。

これから、式(4)が出ます。

そうすると、行列Aのべき乗が求まればなんとかなりそうですね。
ここで、対角行列のべき乗は簡単なことに着目します。
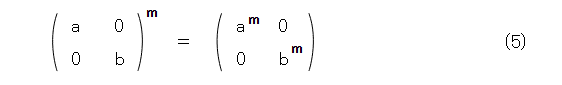
そこで、対角行列Tを座標変換Pで変換して行列Aになったとします。すなわち、図1にのようにします。
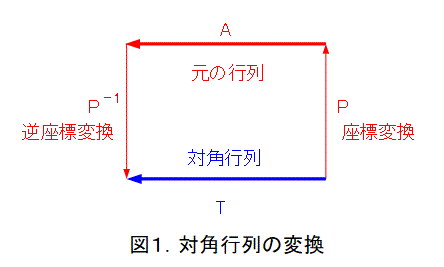
図1を数式化すると式(6)となります。

Aについて解くと式(7)になります。

両辺を n 乗すると式(8)となるので、対角行列Tと、その変換行列Pを求めればよくなりますね。

さて、式(7)から、

そこで、式(10)のようにおきます。
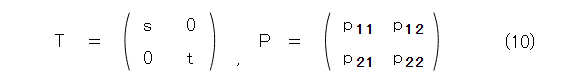
そうすると、式(9)から、
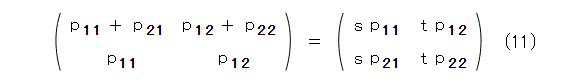
式(11)の両辺の成分を比較して、
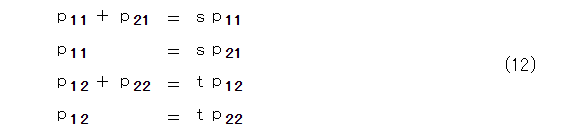
となります。
式(12)から、
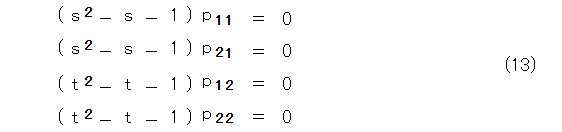
が得られます。
ここで、行列Pは逆行列を持つとしているので、第1列の成分が同時に 0 になることはなく、第2列についても同様なので、式(14)のようになります。

また、 s と t が同一とすると、式(7)の右辺は単位行列のスカラー倍となって成立しません。従って、 s と t は式(15)の相異なる解となります。

また、 s と t はどっちの解を選んでも大して変わらないので、式(16)のようにします。
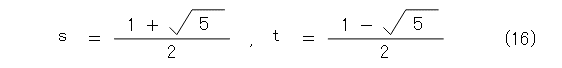
式(16)は複雑なので(本当は描くのが面倒だから)、しばらく s と t の文字のまま使うことにして、式(12)から、行列Pの成分は式(17)のように選べます。

これから、行列Pと、その逆行列は式(18)のようになります。
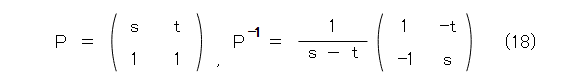
ここまでくると、式(4)、式(8)、式(10)、式(16)、式(18)から、フィボナッチ数列の一般項が式(19)のように求まります。当然ですが、自分で紙に書き、計算して確かめましょう。
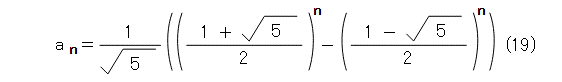
3.フィボナッチ数列の和あれこれ
フィボナッチ数列の一般項である式(19)を見ると、等比数列の差になっています。そうすると、等比数列と似たような性質を持ちそうな気がします。そこで、等比数列の持つ性質を考えてみましょう。
よく知られているのは、等比数列の和ですね。これについて考えてみましょう。初項 1 、項比 r の等比数列の和は式(20)です。
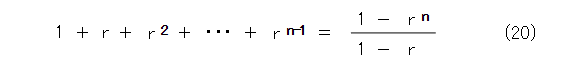
このままでは、何も出てこないので、式(21)のようにおいてみます。

そうすると、式(20)は式(22)のようになります。
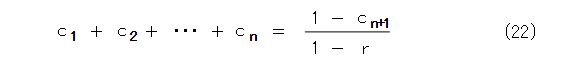
右辺の係数を、適当におくと、式(23)のようになります。
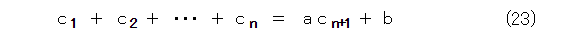
つまり、等比数列の和は、係数と定数を無視すれば、後続項になるということです。不思議なことに、この事実を説明した教師を見たことがありません。なぜでしょう。
フィボナッチ数列は等比数列の差になっているので、和についても似たような感じになります。例えば、式(24)です。
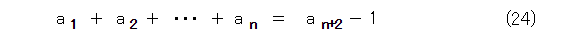
もちろん、腕力でゴリゴリ計算すれば示せるので、読者自身で計算して確かめましょう。
また、以下のようなものもあります。なお、正しいかどうかは自分で確かめましょう。
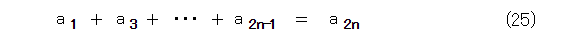
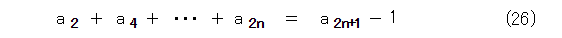
ここで、等比数列は、項を何乗かしても、やはり等比数列になるということに注目すれば、フィボナッチ数列の各項をべき乗化したものの和も似たような性質があると考えられます。実際、式(27)が成り立ちます。これも、正しいかどうかは自分で確かめましょう。
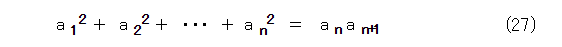
他にも沢山あります。自分で調べたり、考えてみるとよいでしょう。
4.項と項番の関係
フィボナッチ数列の一般項から、腕力でゴリゴリというのばかりでは面白くありませんね。そこで、一般項の形からは見当がつかないような性質に挑戦しましょう。
第122話で、 n が m の倍数の時に、 a n は a m の倍数になるというのをやりました。ここでは、その逆、すなわち、 a n は a m の倍数なら、 n が m の倍数になるかどうかを考えましょう。
では、どうすればよいのでしょうか。一般項を見ても、全然見通しが立ちません。こういうとき、第一選択は、「さっさとあきらめる。」でしたね。いつもそうなんだけども、大人の事情で、解決策を考えなければならないのはどうかと思います(手抜き、ものぐさが得意技なのに)。
それで、大人の事情でしょうがないから、解決策を考えましょう。とにかく、どこから手を付けてよいかが全くわからないので、わかってる事を見てみます。
まず、 n が m の倍数の時に、 a n は a m の倍数になるということを見直します。 n が m の倍数ということから、これは、二つの整数間の性質と考えられますね。そうして、 a n は a m の倍数ということは、二つの項番間の性質が、二つの項間の性質になることと考えられます。ということから、まずは、二つの整数間の性質を考えてみましょう。
二つの整数間の性質でよく知ってるのは、公倍数と公約数でしょう。その上で、公倍数と公約数で、特に重要なのは、最小公倍数と最大公約数ですね。しかし、公倍数の方は、項番が倍数なら項も倍数になるという性質から、考えても面白くなさそうです。そういうことで、最大公約数の方を考えてみましょう。
とりあえず、記述を簡略化し、かっこよく見せるために記号を導入します。 a と b の最大公約数を式(28)のように書きます。

そこで、式(29)のように置きます。つまり、 d を m と n の最大公約数とします。

そうすると、 m と n は d の倍数だから、式(30)が成り立ちます。
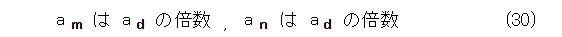
これから、式(31)が出ます。
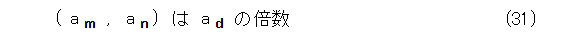
この式を見ていると、式(32)が成り立ちそうな気がしてきます。

さっき導入した最大公約数記号を使うと、式(33)のようにかっこよくなりますね。

それでは、この式が成り立つかどうかを考えましょう。
まずは、最大公約数が必要ですね。2個の整数にユークリッドの互除法を適用すれば最大公約数は求められます。したがって、適当な p 、 q を持ってくれば式(34)のように書けます。当然、詳細な検討は読者の宿題です。なお、ユークリッドの互除法は、第18話に載っています。

次に、ここまでで知っていることは、フィボナッチ数列の一般項と、フィボナッチ数列を連立化した際の係数行列Aです。いま、一般項は使えそうな気がしないので、係数行列Aでなんとかできないかを考えます。Aはべき乗することで、一般項の足がかりになったりしました。とすれば、こいつをべき乗すれば何かが出てくるかもしれませんね。失敗したらまたやり直せばよいので、べき乗の線で考えてみましょう。式(34)をAの肩に乗せてみます。そうすると、式(35)が出てきます。
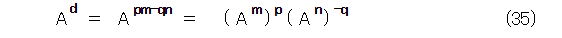
ここで、第122話の式(21)を使うと、式(36)のようになります。
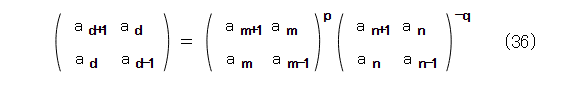
式(36)を眺めると、右辺の行列は、まだべき乗がくっついてうっとおしいですね。なんとかして、なるべく簡単な形にしたいものです。そこで、第122話の式(25)を思い出しましょう。合同式を用いて、無理矢理対角化しています。これを真似てみましょう。
式(36)では、 a n と a m があり、これらを同時に何とかすればよさそうです。そこで、これらの公約数を法に選べば、同時に消せますね。最終的には、式(32)を示したいので、 a n と a m の最大公約数を法に選んでみます。
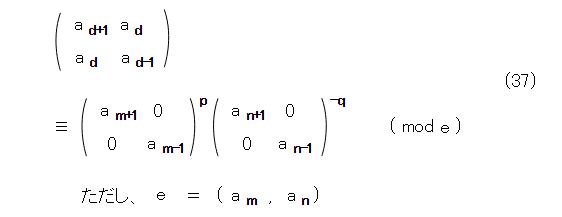
ここで、対角行列のべき乗と積は対角行列になるので、式(37)の左辺も対角行列と合同になります。つまり、式(38)となります。

これから、 a d は e の倍数、つまり、 a m と a n の最大公約数の倍数ということがわかります。
以上のことは見にくいので、まとめて書きます。式(29)、式(37)の但し書きから式(39)、式(31)から式(40)になります。(なんとかはかんとかを割り切るという記号を用いれば、記述が簡単になったので、さっさと出せばよかった。失敗したな。)


式(39)と式(40)とから、両者は一致します。つまり、式(33)が成立します。
こうしてみると、結構、項番の間の関係がフィボナッチ数列の項の関係として保存されていますね。
さて、そういうことがわかって気分が良くなった所で、この章の最初で書いた、 a n は a m の倍数なら、 n が m の倍数になるかどうかを考えましょう。
a n が a m の倍数なら、これらの最大公約数は a m なので式(41)が成立します。
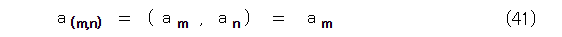
それで、ここからどうしましょうか。とりあえず、考えてるふりして、フィボナッチ数列を見てみます。
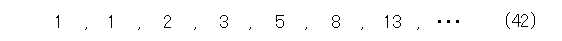
式(42)をみても、なんにも思いつきません。そこで、項を数列っぽく書いてみます。

式(43)を見ると、 a 2 を無視すれば、フィボナッチ数列は増加数列になっています。ということは、式(44)が成り立ちます。
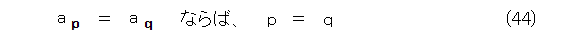
したがって、式(41)が成り立っていれば、式(45)のようになります。

これは、 n が m の倍数であることを示しています。
そうすると、 a 2 を除けば、 a n が a m の倍数なら、 n は m の倍数になることがわかりました。
ところで、 a 2 は 1 なので、 a 3 は a 2 の倍数ですが、 3 は 2 の倍数にはなりません。つまり、 a n が a m の倍数なら、 n は m の倍数になるとは、必ずしも言えません。こんなこと、最初にフィボナッチ数列を具体的に書いてみれば一目瞭然でしたね。いつもやってる、最初に具体例を書いて試すことを省略したため、さんざん苦労して考えてやってきたのに、予想があっさり裏切られ、ひでーめに遭いました。
完
2025年12月1日
著作者 坂田 明治(あきはる)
|