|
第122話
フィボナッチ数列
|

「主な目的」
フィボナッチ数列に限定し、その性質と、性質を調べる方法を紹介します。なお、一般項は求まりますが、一般項を求めて、それを使って性質を調べるとということはしません。
本 文 目 次
1.どうでもいい話
著者 坂田 明治
第122話 フィボナッチ数列
1.どうでもいい話
また。今年もクソ暑い。こんなにクソ暑いのに、ビンボは元気いっぱいで生えてきやがる。また、これから、こいつらと格闘するのか。さっさと全滅しやがれってんだ。
それはともかく、川の土手で、カモたち(種類は不明)の大編隊を見かけた。写真のような編隊を組んで、何波にも渡って大群が飛んでいった。


こいつらが戻ってくるのは、また秋になってからか。
一方で、ドブガモのドブちゃんは残っているはずだけど、どうも様子が変だ。去年まで、田んぼで悪さしてるのが、ちょくちょく見られたのに、なんか見当たらない。色々探し回って、やっと、川の土手の側の田んぼにいるところを見つけた。

しかし、折角見つけたのに、土手の上をジープが走ってきたため、飛んで行ってしまった。

大体、なんでドブガモが居ないのか。気温が高く、田んぼの水温が高いからか。そもそも、ドブガモはどこへ行ってしまったのか。ときどき、飛んでいるのを見かけるから、そんなに遠くへは行ってないと思うが。
飛んでいると言えば、カワウのウっちゃんが飛んでいるところを目撃したので、追ってみたら、電柱に停まって、こんな恰好しやがった。

これ、羽根を乾かしているのだけど、なんか偉そうに、天使にでもなったつもりで羽根を広げているように見えるな。
まあ、しかし、色々な所へ行ってみると、ネギ畑で若いねーちゃんキジを見つけた。

若いねーちゃんキジが単独で見つかるのは珍しいと思って見ていると、案の定、すけべおっさんキジが、隠れながら、そーーーーっと近づいてきやがった。

この後、やっぱり思った通り、若いねーちゃんキジは逃げてしまった。
2.ウサギかネズミのつがいの例
昔(一体、何十年前だよ)のことだから記憶が曖昧だけども、1つがいのウサギだかネズミだかが、1カ月毎に1つがいの子を産んで、そいつらも1カ月毎に1つがいの子を産んで増えるとすれば、このつがいの数はフィボナッチ数列になるとかなんとかいうものだったと思います。
これ、とにかくご都合主義で色々なことは無視しています。つまり、近親相姦を引き起こして弱くなり、死産しやすくなるとか、その他そういう諸々のことは無視です。
大体、産まれてから1カ月で性成熟して出産ってなんだよ。いくらなんでもウサギではないでしょう。ネズミなら、ハツカネズミというのがいるからなんとかなるかも(ならねーよ)。ハツカネズミというのは、妊娠期間が二十日で、それが名前の由来なんだけど、産まれてから十日で性成熟っていうのは無理でしょうね。
まあ、いいや。都合の悪いことは無視で、ネズミということにして、つがいの数が順にどうなるか書いてみましょう。
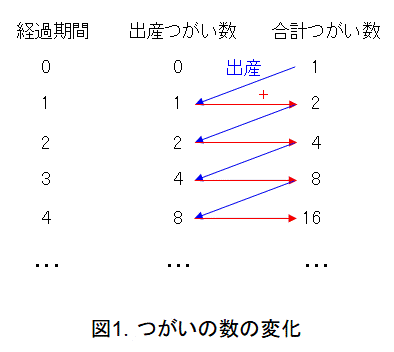
倍々で増えることを、ネズミ算という位だから、図1のようになるのは当然でしょうね。
そもそも、フィボナッチ数列というのは、式(1)の漸化式と初期値による数列なので、全然、ネズミのつがいの数では、フィボナッチ数列にはなりません。
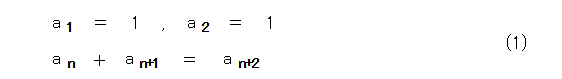
一応、図1との比較のため、最初の項を書いてみます。
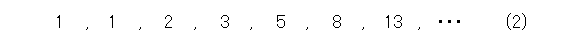
やっぱり、どう考えても図1に出てくる数列はフィボナッチ数列ではないですね。「全く、嘘八百じゃねーか。どこにフィボナッチ数列が出てくるんだ。」と文句を付けたくなります。更に、いつもなら こういうときの第一選択は、「さっさとあきらめる。」ことでした。
そこで、今回は、どっかの国で最も流行っている、「最初に結論ありき。」という考えのもと、なんでもいいからこじつけて、この結論、つまり、無理やりフィボナッチ数列が出てくるようにしてみましょう。
式(1)をよく見てみると、現時点に関係するのは前2つですね。ということは、この制限を加えてみたらどうでしょうか。前2つ以前が消滅するように話を捻じ曲げます。
つまり、現時点は後2つまでしか関与せず、後3つ目では消え去っているようにすればよさそうです。ということで、ネズミの寿命に制限を設けてみましょう。
ネズミの寿命を2カ月とし、1カ月目と2か月目につがいを産んで寿命を迎えるとします。こうして、つがいの数の変化を書いてみます。
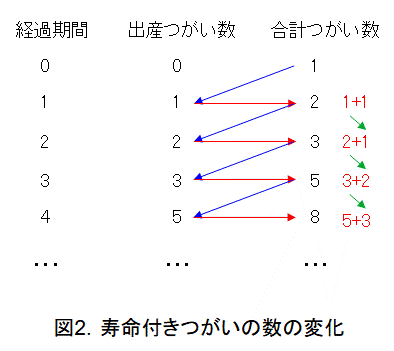
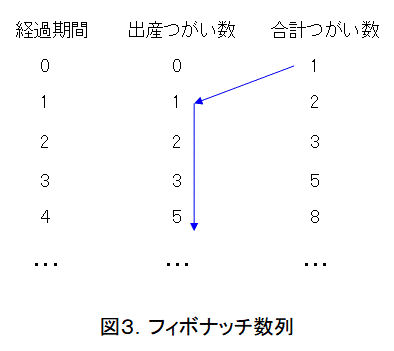
図2の合計つがい数の右に書かれた赤い式は、第1項が今回の出産つがい数、第2項が前回のつがい数です。要するに、2回目のつがい出産後、寿命で消滅します。
こうすると、フィボナッチ数列っぽいのが見えてきましたね。でも、まだ、出産つがい数の列と合計つがい数の列では式(2)のフィボナッチ数列にはなりません。ここで、欠けているのは初項なので、図3の青の矢印のように取り出せばフィボナッチ数列になります。
ということで、まとめると、1つがいのネズミが1カ月毎に1つがいを産み、以下、産まれたつがいも1か月毎に1つがいを産み、更に、これらのネズミの寿命は2カ月で、2か月後につがいを生むと消滅するときに、1つがいから始めて、1カ月ごとに産まれてくるつがいの数はフィボナッチ数列となる。ここで、近親相姦や、その他諸々の問題は無視する。
全くの話、こんな頭があったら、最初に結論ありきでこじつけるよりも、もっと柔軟に、話を変えた方が簡単じゃないかと思う。実際、フィボナッチ数列の例は色々あるから、それを持ってくれば済むのにね。
3.漸化式の連立化と係数行列の性質
さて、フィボナッチ数列は式(1)の差分方程式だから、第114話、第115話を参考にすれば、簡単に一般項が求まります。当然、一般項を導き出すのは読者の宿題です。なお、本稿では一般項を求めたり、その結果を使ったりしません。
ここでは、連立化して、係数行列の性質を見ていきましょう(第115話参照)。
まず、式(3)のようにおきます。

すると、式(1)の漸化式部分は式(4)のようになります( n を n-1 に繰り下げている)。

式(3)、式(4)から、行列表示したものが式(5)です。
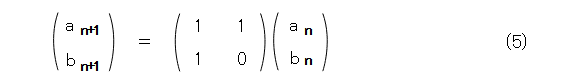
この係数行列、何か感じるものがありますね。とりあえず、式(6)のようにおいてみましょう。

見てても始まらないので、試しに2乗してみます。
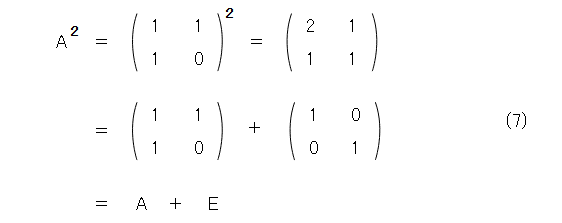
ここで、Eは2次の単位行列です。
式(7)を見ていると、両辺に、A n を掛けたくなりますね。
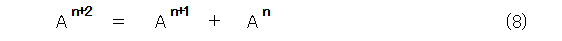
ほら、行列の間の式も、フィボナッチ数列の漸化式(式(1))と同じ形ですね。こんな面白い性質を持っていたのでした。
それを確かめてみましょう。まずは、式(9)のように置きます。

そして、式(10)を成分で書いて、式(11)を出します。

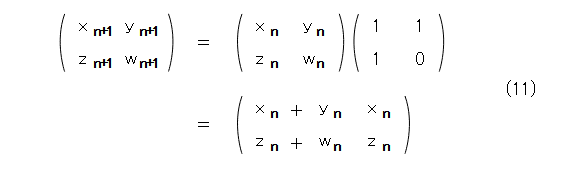
式(11)の成分を比較して、
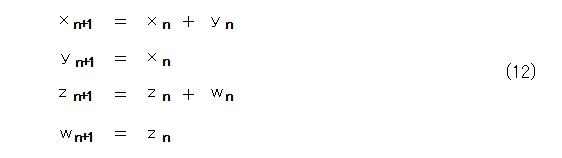
となります。なんかフィボナッチ数列の漸化式を連立化したものが出てきました。
文字が多すぎるので、何とかしてもっと減らすことを考えましょう。
元々、行列Aは対称行列だったので、転置行列をとっても変わりません。

この性質は n 乗しても変わらないので、式(14)が成り立ちます。

したがって、式(15)が成り立ちます。

式(12)と式(15)とから、式(16)の形になります。
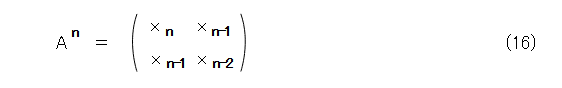
式(8)を成分で比較すれば、式(16)の各成分はフィボナッチ数列の漸化式を満たしていることが明らかです。そうすると、式(1)のフィボナッチ数列との差は、いわゆる初期値の取り扱いだけの差から生じることになります。ただし、式(6)で、Aの2行2列目の成分は 0 であるため、結論ありきのようなこじつけが必要です。
そこで、勝手に、フィボナッチ数列の第 0 項を 0 として追加してしまいます。この場合、式(1)の漸化式から、式(17)のようになります。要するに、頭に 0 を追加しても何の矛盾もしません。

また、式(6)と式(16)とから、式(18)のようになります。
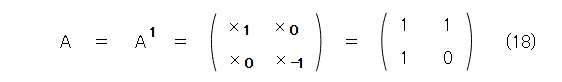
そこで、式(18)の各要素を比較した上で、フィボナッチ数列の漸化式を適用すると式(19)が出てきます。
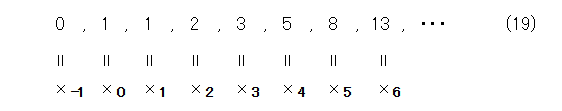
これから、 x n と a n との関係は式(20)のようになります。

こうして、係数行列の正体が明らかになりました。
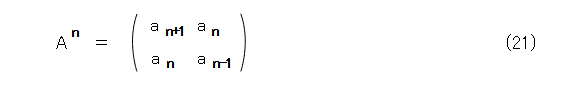
4.フィボナッチ数列の持つ性質
さて、フィボナッチ数列は、色々面白い性質を持っています。それらを少し考えてみましょう。こういうのを調べるとき、例えば、数列の順番が持っている関係が、フィボナッチ数列の項の間にも成り立つかなどです。
ある程度、項を先まで書かなければ傾向が見えませんので、式(17)の7項目(少なすぎる。手抜きだ。ちゃんとやりたい人は、もっと先まで書いて調べよう。)までで無理やり推定しましょう。
順番が7 までなので、こんなのでなんか関係があるものはと言っても、 2 と 3 を掛けたら 6 になるというぐらいしかないじゃないか。というのは無視して、 2 項目と 3 項目の項を見ても、 1 と 2 で、 6 項目は 8 だから、掛けたものにはならないけど、 6 項目は、 2 項目と 3 項目の倍数になっています。
すげー、いい加減な傾向の見方によって、 n が m の倍数の時に、 a n は a m の倍数になると予想されますね(こんなの、最初から結果を知っていて、最初に結論ありきとやってるだけじゃないか)。
まあ、とにかく、この予想にしたがって考えてみます。まず、 n が m の倍数だから、式(22)のように書けます。

式(21)があるので、とりあえず、これを使ってみます。
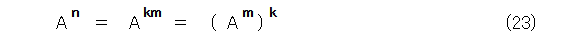
なので、式(24)が成り立ちます。
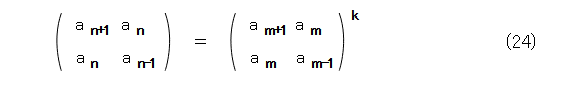
ここで、行列の合同式を、各要素がそれぞれ合同なこととすると、
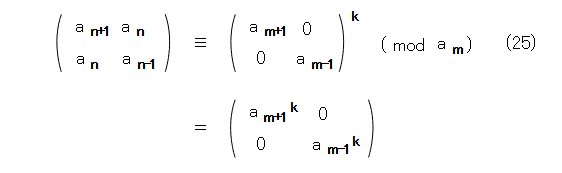
これから、式(26)が出ます。

これは、 a n は a m の倍数になるということですね。
次に、一見「えっ。」っと思うけれども、よく考えると、「なんだ当たり前か。」という性質を述べましょう。そのために、心の準備じゃなくて、用語の準備をします。
フィボナッチ数列の各項をフィボナッチ数ということにします。
こうすると、全ての自然数は、異なるフィボナッチ数の和で表されます。なんか、どきっとするような性質ですね。でもこれ、よく考えると、当たり前の性質です。式(1)から、フィボナッチ数はどんどん増加していくので、任意の自然数 x に対し、適当な n をとると式(27)が成り立ちます。

これから、ただちに式(28)が出ます。
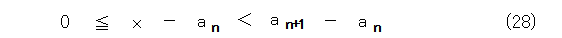
式(1)の漸化式から式(29)となります。
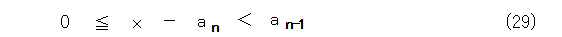
すると、適当な m をとると式(30)が成り立ちます。
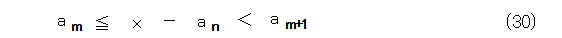
以上と同じようにして、式(31)が出ます。
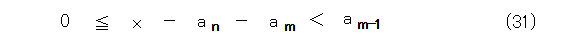
以下同様にして、続けていけば、不等式の最右辺は減少していき、やがて 0 になります。
そうすれば、式(32)のようになって、異なるフィボナッチ数の和で表されます。
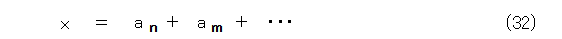
ちなみに、この性質はフィボナッチ数列の漸化式からの直接の帰結となります。ということで、当たり前の性質ですよね。
他にも、フィボナッチ数列の性質は沢山あるので、自分で探してみましょう。
完
2025年7月20日
著作者 坂田 明治(あきはる)
|